Tags
Key points:
- The predetermined set of game rules are easily understood. 21-24-27 is easy to play.
- The players agree. Under certain circumstances, the dealer does not consult with the player for a decision on how to play the player’s hand. The player must play the player’s hand a certain way.
- This agreement enables the players. The dealer can conduct 21-24-27 games at a faster pace than would otherwise be possible. Thereby, making the game more profitable for the host. The players can enjoy playing a fast paced game without suffering the unnecessary burden of consulting with the dealer for every decision on how to play the player’s hand.
- The 21-24-27 game is mostly invulnerable to players who employ card-counting and betting strategies.
Method Of Play
21-24-27 is a comparing card game belonging to the Finnish 27™ family of table-card games.
21-24-27 is easy to play. The method of play can be broken down into a series of steps.
The first step is. The host furnishes a table, a dealer, chips, and at least one deck of playing cards and a player buys chips and sits down to play. All players agree to play as specified by the predetermined set of game rules. The predetermined set of game rules specify. A standard deck of playing cards consists of thirteen ranks of each of four French suits plus two jokers for a total of fifty four cards.
The next step is. A player must place a game wager. Chips would most likely be used. Chips stand in for the value of the game wager. The player buys chips from the host. The player places the chips on the table.
Afterward, the dealer deals initial hands to designated spots on said table. The initial hands consist of a player’s initial hand and a dealer’s initial hand. Each initial hand consists of two cards. The two cards are dealt face up. That is. The two cards have front sides. The front sides bear markings. The markings indicate the ranks and suits of said cards. The markings are exposed and visible to players.
The knowledge of the ranks of said cards enables players. Players can determine the numeric values of said cards. Each joker has a value of 0. Each Ace has a value of 1 or 14. Each King has a value of 13. Each queen has a value of 12. Each Jack has a value of 11. Each of the remaining cards bears a number and suit. The number represents the rank of the card. The ranks are 2, 3, 4, 5, 6, 7, 8, 9, and 10. Each of the remaining cards bears a number of pips. The number of pips is equal to the number of the rank. Each of the remaining cards has a value. The value is equal to the number of the rank and the number of pips.
Comparing card games belonging to the Finnish 27™ family of table card games can be played with any style of markings including the ubiquitous Anglo-American style of markings. However, the Anglo-American style of markings uses the letters J, Q, K, and A on the Jacks, Queens, Kings, and Aces respectively. The Finnish style of markings uses the numbers 11, 12, 13, and 1 on the Jacks, Queens, Kings, and Aces respectively. The Finnish style of markings best suggests the numeric values of the cards in comparing card games belonging to the Finnish 27™ family of table-card games. For that reason, the Finnish style deck of cards is preferred.
Knowledge of the numeric values of the cards and simple addition enables the players. The players can determined the numeric value of the hand. The numeric value of the hand is also known as the hand total.
Let us suppose. A hand includes an ace. A value of 14 can be assigned to the ace without causing the value of the hand total to exceed 27. In that event, the players would agree. The ace is known as a high ace. The value of the high ace is 14.
Let us suppose. A hand includes an ace. A value of 14 can not be assigned to the ace without causing the hand total to exceed 27. In that event, the players would agree. The ace is known as a low ace. The value of the low ace is 1.
Let us suppose. A hand includes a high ace. In that event, the hand is known as a soft hand. The hand total is known as a soft total.
Let us suppose. A hand does not include a high ace. In that event, the hand is known as a hard hand. The hand total is known as a hard total.
The dealer’s initial hand consists of two cards. The two cards are dealt face up. The act of dealing both cards in the dealer’s initial hand face up is known as double exposure. Double exposure is an attribute of the 21-24-27 game. Double exposure offers the players an opportunity. The players can determine the numeric values of the cards in the dealer’s initial hand. Knowledge of the numeric values and the use of simple addition enable players. Players can determine the dealer’s hand total. The dealer’s hand total is the hand total of the dealer’s hand.
Let us suppose. The dealer deals an initial hand. The initial hand consists of a high ace and a king in any order. In that event, the players would agree. The numeric values of the cards in the initial hand add to a hand total of 27. The initial hand is known as a Finnish 27 hand. The Finnish 27 hand is a predetermined-winning-complete hand. The dealer would immediately determine the outcome of the game.
Let us suppose. The player’s initial hand is a Finnish 27 hand and the dealer’s initial hand is not a Finnish 27 hand. In that event, the outcome of the game would be. The player’s Finnish 27 hand wins. The dealer would pay the player one to one odds on the game wager. The game would be over.
Let us suppose. The dealer’s initial hand is a Finnish 27 hand and the player’s initial hand is not a Finnish 27 hand. In that event, the outcome of the game would be. The dealer’s Finnish 27 hand wins. The dealer would collect the game wager. The game would be over.
Let us suppose. Both initial hands are Finnish 27 hands. In that event, the outcome of the game would be a stalemate. The Finnish 27 hands would tie. The dealer would return the game wager to the player. The game would be over.
Let us suppose. A Finnish 27 hand has not been dealt. In that event, the game would continue. The next step would be. The players take turns playing their hands. The player would go first. The dealer would determine whether or not. The dealer consults with the player for a decision on how to play the player’s hand. Let us suppose. The dealer does consult with the player for a decision on how to play the player’s hand. In that event, the player would have two options. The two options would be hit and stand. Let us suppose. The player decides to hit. In that event, the dealer would add one additional card to the player’s hand. Let us suppose. The player decides to stand. In that event, the dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The player’s hand is complete. The player’s hand total does exceed 27. In that event, the player’s hand would be a predetermined-losing-complete hand. The outcome of the game would be the dealer’s hand wins. The dealer would collect the game wager. The game would be over.
Let us suppose. The player’s hand is complete. The player’s hand total does not exceed 27. In that event, the game would continue. The next step would be. The dealer would play the dealer’s hand. The players would agree. The dealer must play the dealer’s hand in accordance with a predetermined strategy. The predetermined strategy is.
Let us suppose. The dealer’s hand of cards does not include a high ace. The dealer’s hand of cards is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is less than 21. In that event, the players would agree. The dealer must hit. The dealer would add one card to the dealer’s hand of cards.
Let us suppose. The dealer’s hand of cards does not include a high ace. The dealer’s hand of cards is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is at least equal to 21. In that event, the players would agree. The dealer must stand. The dealer would add nothing to the dealer’s hand. The dealer’s hand would be complete.
Let us suppose. The dealer’s hand of cards does include a high ace. The dealer’s hand of cards is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is less than 24. In that event, the players would agree. The dealer must hit. The dealer would add one card to the dealer’s hand.
Let us suppose. The dealer’s hand of cards does include a high ace. The dealer’s hand of cards is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is at least 24. In that event, the players would agree. The dealer must stand. The dealer would add nothing to the dealer’s hand. The dealer’s hand would be complete.
Please understand. The predetermined set of game rules specifies three target values. The three target values are 21, 24, and 27. Some of the dealer’s hands are hard hands. That is. Some of the dealer’s hands do not include a high ace. The target value for the play of the dealer’s hard hands is a hard total of at least 21. Some of the dealer’s hands are soft hands. That is. Some of the dealer’s hands do include a high ace. The target for the play of the dealer’s soft hands is a soft total of at least 24. The dealer uses hand totals. The dealer determines the outcome of the game. The dealer compares hand totals to a target numeric sum of 27. The closest to 27 without going over wins, and ties are a stalemate. For that reason, the target numeric sum of the game is 27. The name of the game 21-24-27 denotes the specification of these three targets.
Let us suppose. The dealer’s hand is complete. The dealer’s hand total does exceed 27. In that event, the dealer’s hand would be a predetermined-losing-complete hand. The outcome of the game would be the player’s hand wins. The dealer would pay the player one to one odds on the game wager. The game would be over.
Let us suppose. The player’s hand is complete. The player’s hand total does not exceed 27. The dealer’s hand is complete. The dealer’s hand total does not exceed 27. In that event, the game would continue. The next step would be. The dealer would determine the outcome of the game. The dealer would compare hand totals to a target numeric sum of 27. The closest to 27 without going over would win, and ties would be a stalemate. Let us suppose. The dealer’s hand total is closer to 27 than is the player’s hand total. In that event, the outcome of the game would be. The dealer’s hand wins. Let us suppose. The player’s hand total is closer to 27 than is the dealer’s hand total. In that event, the outcome of the game would be. The player’s hand wins. Let us suppose. The dealer’s hand total and the player’s hand total are an equal distance from 27. In that event, the outcome of the game would be a stalemate.
The final step is. The dealer resolves the game wager. Let us suppose. The outcome of the game is the dealer’s hand wins. In that event, the dealer would collect the game wager. Let us suppose. The outcome of the game is the player’s hand wins. In that event, the dealer would pay the player one to one odds on the game wager. Let us suppose. The outcome of the game is a stalemate. In that event, the dealer would return the game wager to the player.
Optional Rules Speed Up The Pace Of Play
The act of consulting with the player for a decision on how to play the player’s hand takes time. Sometimes the correct decision is obvious. The act of consulting with the dealer for every decision on how to play the player’s hand would slow down the pace of play. It would put an unnecessary burden on both the player and the dealer. For those reasons, the players would agree. Under certain circumstances, the dealer does not consult with the player for a decision on how to play the player’s hand. The player must play the player’s hand a certain way. This agreement enables the players. The dealer can conduct 21-24-27 games at a faster pace than would otherwise be possible. Thereby, making the game more profitable for the host. The players can enjoy playing a fast paced game without suffering the unnecessary burden of consulting with the dealer for every decision on how to play the player’s hand.
It appears. In about 1 out of every 5 games, the cards in the dealer’s initial hand add to a hand total. The hand total is high enough. A target value for the play of the dealer’s hand has been met. Upon the dealer’s turn to play, the dealer will stand. The dealer’s initial hand is a complete hand.
Let us suppose. The dealer’s initial hand is a complete hand. In that event, the players would agree. Under certain circumstances, the dealer does not consult with the player for a decision on how to play the player’s hand. The player is required to play the player’s hand a certain way. Those certain circumstances and certain ways are.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand total is less than the dealer’s hand total. In that event, the players would agree. The player’s hand total is not high enough. The player must hit. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add one card to the player’s hand.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand total is greater than the dealer’s hand total. In that event, the players would agree. The player’s hand total is high enough. The player must stand. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is at least 25. The hard total is equal to the dealer’s hand total. In that event, the players would agree. The hard total is high enough. The player must stand. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is 27. The soft total is equal to the dealer’s hand total. In that event, the players would agree. The player’s hand total is high enough. The player must stand. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The dealer’s initial hand is a complete hand. In that event, the players would agree. Under certain circumstances, the dealer does consult with the player for a decision on how to play the player’s hand. Those certain circumstances are.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is less than 25. The hard total is equal to the dealer’s hand total. In that event, the players would agree. The dealer does consult with the player for a decision on how to play the player’s hand.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is less than 27. The soft total is equal to the dealer’s hand total. In that event, the players would agree. The dealer does consult with the player for a decision on how to play the player’s hand.
It appears. In about 4 out of every 5 games, the cards in the dealer’s initial hand add to a hand total. The hand total is not high enough. A target value for the play of the dealer’s hand has not yet been met. Upon the dealer’s turn to play, the dealer will hit. That is. The dealer will add at least one additional card to the dealer’s initial hand. The dealer’s initial hand is not yet a complete hand.
Let us suppose. The dealer’s initial hand is not yet a complete hand. In that event, the players would agree. Under certain circumstances, the dealer does not consult with the player for a decision on how to play the player’s hand. The player is required to play the player’s hand a certain way. Those certain circumstances and certain ways are.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a hard hand. The numeric values of the hard hand add to a hard total. The hard total is less than 15. In that event, the players would agree. The hard total is not high enough. The player must hit. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add one card to the player’s hand.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is less than 23. In that event, the players would agree. The soft total is not high enough. The player must hit. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add one card to the player’s hand.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is at least 25. In that event, the players would agree. The hard total is high enough. The player must stand. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is 27. In that event, the players would agree. The soft total has reached the target value of 27. The player must stand. The dealer would not consult with the player for a decision on how to play the player’s hand. The dealer would add nothing to the player’s hand. The player’s hand would be complete.
Let us suppose. The dealer’s initial hand is not yet a complete hand. In that event, the predetermined set of game rules specifies. Under certain circumstances, the dealer does consult with the player for a decision on how to play the player’s hand. Those certain circumstances are.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a hard hand. The numeric values of the cards in the hard hand add to a hard total. The hard total is at least 15. The hard total is not more than 24. In that event, the players would agree. The dealer would consult with the player for a decision on how to play the player’s hand.
Let us suppose. The dealer’s initial hand is not yet a complete hand. The player’s hand is a soft hand. The numeric values of the cards in the soft hand add to a soft total. The soft total is at least 23. The soft total is not more than 26. In that event, the players would agree. The dealer would consult with the player for a decision on how to play the player’s hand.
Basic Strategy
I wrote a series of computer programs. I had the ability. I am grateful. The series of computer programs enabled me. I input the predetermined set of game rules for a game of 21-24-27. The predetermined set of game rules specified. The host provides one standard deck of playing cards. The series of computer programs enabled me. I found the best strategy for the play of the player’s hand. The best strategy for the play of the player’s hand is known as the “basic strategy”. The basic strategy is often displayed in the form of a table of values. The table below shows the basic strategy for the play of the game of 21-24-27.


A brief examination of the basic strategy for the play of the player’s hand in a game of 21-24-27 reveals. The strategy for the play of the player hard hands often calls for the player to hit until the player’s hand total has reached at least 22. The act of adding a high denomination card to the player’s hand can cause the player hand total to exceed 27 before the player’s hand total reaches the target of at least 22. For that reason, the act of having a fewer number of high denomination cards in the stack increases the expected value of the game. The act of adding a low denomination card to the player’s hand can not cause the player’s hand total to exceed 27 before the player’s hand total reaches the target of at least 22. For that reason, the act of having a higher than normal number of low denomination cards in the stack increases the expected value of the game.
However, that’s not the whole story. The dealer must stand with a hard total of at least 21. The dealer must stand for a soft total of at least 24. Both of the cards in the dealer’s initial hand are dealt face up. For that reason, the players can know whether or not. The dealer’s initial hand is a complete hand. Let us suppose. The dealer’s initial hand is a complete hand. In that event, upon the dealer’s turn to play the dealer’s hand, the dealer must stand. Knowledge of these facts confers a huge advantage upon the player.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand total is less than the dealer’s hand total. In that event, the player must play the player’s hand a certain way. The player must hit. The dealer adds a card to the player’s hand. The player does have a chance to improve the player’s hand. The player’s hand could possibly tie or win the game.
Let us suppose. The dealer’s initial hand is a complete hand. The player’s hand total is greater than the dealer’s hand total. In that event, the player must play the player’s hand a certain way. The certain way is. The player must stand. The player’s hand is complete. Upon the dealer’s turn to play, the dealer must play the dealer’s hand a certain way. The dealer must stand. The dealer’s hand is complete. The dealer does not have a chance to improve the dealer’s hand. The dealer’s hand could not possibly tie or win the game.
It appears. The dealer’s initial hand is complete in an average of about 20% of all games. When it does happen, the player enjoys an advantage over the dealer. The advantage is. The player does have a chance to improve the player’s hand when the dealer’s hand total is greater than the player’s hand total. The dealer does not have a chance to improve the dealer’s hand when the dealer’s hand total is less than the player’s hand total.
The advantage only ever manifests when the dealer’s initial hand consists of two high denomination cards. For that reason, it appears. The act of having a greater than normal abundance of high denomination cards in the stack has its advantages and disadvantages. The advantages balance out some of the disadvantages. The act of removing cards from the stack causes changes in the expected value of the game. The changes are small.
The Expected Value of the Game and The House Edge
The mathematics of the game should be. The host retains a percentage of the game wager in the long run with strictly average luck. This percentage is called the house edge. The set of computer programs and knowledge of the basic strategy enabled me. I calculated an estimate of the expected value of the game. For the purposes of the act of calculating the estimate of the expected value of the game, it was assumed. The player always uses the basic strategy when making decisions on how to play the player’s hand. The estimate of the expected value of the game was found to be -1.15%. That is. Players can expect to lose an average of at least 1.15% of the value of all game wagers in the long run with strictly average luck.
The expected value of the game is the flip side of the house edge. For that reason, the act of multiplying the estimate of the expected value of the game by -1 yields a product. The product is an estimate of the house edge. The estimate of the house edge is 1.15%. That is. The house can expect to gain an average of at least 1.15% of the total value of all game wagers in the long run with strictly average luck.
The Definition Of The Stack
The method for the conduct of a game of 21-24-27 frequently specifies a step. The step is. The dealer adds a card to a hand of cards. Please understand. To do so, the dealer removes a card from a stack of cards. The stack consists of a portion of the cards in use. In this case, the cards in use are the cards of a standard deck of cards. The dealer draws a card from the stack whenever the dealer adds a card to a hand of cards. Once the card is added to a hand of cards, the card is no longer part of the stack. The hands of cards are displayed on the top of a game table. The hands of cards are not part of the stack. After a game concludes, the dealer removes the hands of cards from the top of the game table. The dealer adds the hands of cards to a discard pile. The discard pile is not part of the stack.
The Effect of Removal Of Cards From The Stack On The Expected Value Of The Game
Let us suppose. The dealer does not immediately shuffle the cards upon the conclusion of a game. The dealer uses the stack. The dealer conducts a subsequent game. In that event, it would be logical to infer. The act of removing a card from the stack in the previous game would have an effect on the expected value of the game in the subsequent game. The rank of card would determine the effect. The act of removing certain ranks of cards from the stack would increase the expected value of the game. The act of removing certain other ranks of cards from the stack would decrease the expected value of the game. The act of removing still other ranks of cards from the stack would have little or no effect on the expected value of the game.
Comparing 21-24-27 to Blackjack (21)
Card games belonging to the Blackjack family and card games belonging to Finnish 27™ family of table card games have many similarities and differences. The similarities include. Card games belonging to both families are target numerical sum games. That is. Cards have numeric values. The players add up the numeric values of the cards in the hand. Thereby, the players determine the hand total. The players compare the hand total to a target numeric value. The differences include. In card games belonging to the Finnish 27™ family of table-card games, the target is 27. In card games belonging to the Blackjack family of table-card games, the target is 21. The object of these card games is. Win a game wager. The The players do so by acquiring a hand of cards with a higher value than the dealer’s hand of cards. The predetermined set of game rules varies amongst card games belonging to the Finnish 27™ family of table card games. In 21-24-27 and in most, if not all, Blackjack games, the rule is. Closest to the target value without going over wins and ties are a stalemate.
Card Counting Systems And The Obvious Question
It appears. Some blackjack players have used knowledge of the composition of the stack. They have. Estimated the expected value of the game. Invented card counting strategies. Counted cards. The card counting strategies enabled them. They kept track of the cards removed from the stack. Thereby, they kept track of the composition of the cards in the stack. Some blackjack players have. Capitalized when it appeared. The composition of the cards in the stack favored the player. They invented betting strategies. Their betting strategies enable these blackjack players. These blackjack players bet more when it appears to them. The composition of the stack favors the player.
21-24-27 and blackjack are both target-numerical-sum games. Some people claim. The act of employing a card counting strategy while playing blackjack is profitable for the player in the long run with strictly average luck. An obvious question is. Would the act of employing a card counting strategy while playing 21-24-27 be profitable for the player in the long run with strictly average luck?
Use Of A High-Speed Game Simulator To Answer The Question
The set of computer programs enabled me to answer this question. I loaded the basic strategy and the predetermined set of game rules into a high-speed game simulator. Thereby, the high-speed-game simulator enabled me. I programmed a computer-controlled dealer to conduct a 21-24-27 game in accordance with the above-described predetermined set of game rules. The high speed game simulator enables users. Users can program a computer-controlled player. Users can define a card counting strategy, a betting strategy, and a playing strategy. The computer-controlled player will. Count cards in accordance with the user-defined-card-counting strategy. Make decisions about how many credits to bet in accordance with the user-defined-betting strategy. Make decisions on how to play the player’s hand in accordance with the user-defined-playing strategy.
Method For Inventing A Card Counting Strategy For 21-24-27
The high speed game simulator includes a software means. At the start of each round of play, and for every rank of card, the software means finds a percentage value for the frequency of the occurrence of the rank of card in the stack. The software means finds a percentage value for the frequency of the occurrence of the rank of card in a complete standard deck. The software means subtracts the percentage value for the frequency of the occurrence of the rank in the complete standard deck from the percentage value for the frequency of the occurrence of the rank in the stack. The subtraction operation yields a percentage value for the difference in the frequency of the occurrence of the rank of card. At the end of each round of play, the high speed game simulator finds a weighted value for the outcome. Let us suppose. The outcome of the game is the dealer’s hand wins. In that event, the software means finds. The value for the outcome is -1. Let us suppose. The outcome of the game is a stalemate. In that event, the software means finds. The value of the outcome is 0. Let us suppose. The outcome of the game is the player’s hand wins. In that event, the software means finds. The value of the outcome is 1. The software means multiplies the value of the outcome by the value of the game wager. The product of this multiplication operation is a weighted value for the outcome of the game. For every rank of card, the software means multiplies the weighted value for the outcome of the game by the percentage value for the difference in the frequency of the occurrence of the rank of card. The product of this multiplication operation is a decimal value. For every rank of card, the software means adds the decimal value to an ongoing summation of values. A number of rounds of play have elapsed since the start of the simulation. The software means divides the ongoing summation of values by the number of rounds of play. The quotient of this division operation is a decimal value. The decimal value is a measure of the effect on the expected value of the game caused by the act of removing one card of the rank from the stack. For each rank of card, it appears. Over time, the average decimal value converges upon an optimal decimal value.
Programming The High Speed Game Simulator To Conduct A First Game Simulation
The high-speed game simulator enabled me. I programmed the high-speed-game simulator to conduct a simulation. I programmed a computer-controlled dealer. I defined a predetermined set of game rules. The predetermined set of game rules was the above described predetermined set of game rules for a 21-24-27 card game. The computer-controlled dealer conducted 21-24-27 card games in accordance with the predetermined set of game rules. A computer-controlled player played heads up against the dealer. I programmed a computer-controlled player. The computer-controlled player employed a betting strategy. The betting strategy was. The computer-controlled player always bets table minimum. The computer-controlled player employed a playing strategy. The playing strategy was basic strategy. I programmed the high-speed game simulator to simulate one hundred sessions of play. I defined each session of play as ten-million rounds of play. The computer-controlled players played a total of one-billion rounds of play. The game simulator saves a summary of the final simulation results to a text file. The image below shows a portion of the text file.

Discussion of Game Simulation Results: The House Edge
The game simulation conducted 100 sessions. Each session consisted of 10,000,000 rounds of play. It appears. The game simulation results reveal. The change in the (player’s) purse was an average of -109,591.95 credits after 10,000,000 rounds of play. That is. After 100 sessions of 10,000,000 rounds of play each, the computer-controlled player lost a number credits more than the player won. The number of credits was 10,959,195. This works out to an expected value of the game wager of -1.1% and a house edge of about +1.1%
The set of computer programs enabled me. I made an estimate of the house edge by means of an abbreviated combinatorial analysis. This estimate was 1.15%. The estimate is close to game simulation results of 1.1%. For that reason, it would be logical to infer. The game simulator and set of computer programs are working well in coordination as hoped and expected. That is. The software is providing us with results. The game simulation results agree with the abbreviated combinatorial results.
Discussion of Game Simulation Results: Average Number of Consultations
Under certain circumstances, the computer-controlled dealer consulted with the computer-controlled player for a decision on how to play the player’s hand. An examination of the game simulation results reveals. The computer-controlled dealer consulted with the computer-controlled player for a decision on how to play the players hand an average of 1.04 times per each player’s-complete hand. The predetermined set of game rules included a subset of game rules. The subset of game rules specified. Under certain circumstances, the computer-controlled dealer did not consult with the computer-controlled player for a decision on how to play the player’s hand. The computer-controlled player was forced to play the player’s hand a certain way. An examination of game simulation results not shown here reveals. Without the inclusion of the subset of game rules, the average number of consultations per each player’s complete hand increases to 1.89 times per each player’s-complete hand. Accordingly, it appears. The inclusion of the subset of games rules within the predetermined set of game rules significantly reduces the number of consultations per each player’s-complete hand. From these results, it would be logical to infer. The inclusion of the subset of game rules within the predetermined set of game rules would significantly speed up the pace of play in a live casino environment.
Discussion of Game Simulation Results: The Effect of Removal
A table of values appears at the bottom of this image. The table has a title. The title reads. Change in expected value of the game wager caused by the removal of one card of a given denomination from the stack during this game simulation. This table of values is where. For each denomination of card, the high-speed game simulator displays the average decimal value for the changes in the expected value of the game caused by the removal of one card of the denomination from the stack. Please understand. Denomination is another word for card rank. Over time these average decimal values converge upon the optimal decimal values. After one-billion rounds of play, it would be logical to infer. These average decimal values are near optimal.
Certain cards have certain ranks. The certain ranks are ace, two, three, four, five, and six. It appears. The act of removing one of these certain cards from the stack results in a negative change in the expected value of the game. From this, it would be logical to infer. The expected value of the game increases when these certain ranks are found in less than normal abundance within the stack. The expected value of the game decreases when these cards are found in greater than normal abundance within the stack. Please understand. For each rank of card, normal abundance is defined as the abundance of the rank of card found in one standard deck of cards.
Certain cards have certain ranks. The certain ranks are joker, seven, eight, nine, ten, jack, queen, and king. It appears The act of removing one of these certain cards from the stack results in a positive change in the expected value of the game wager. From these facts, it would be logical to infer. The expected value of the game increases when these cards are found in less than normal abundance within the stack. The expected value of the game decreases when these certain ranks are found in greater than normal abundance within the stack.
The Invention Of A Card Counting System For Use While Playing 21-24-27
For every denomination of card, the game simulation results revealed. The removal of one card of a given denomination from the stack caused a change in expected value of the game wager. These values for the changes in the expected value of the game wager can become the basis for the invention of a card counting system.
However, human players count integers when using a card counting system. Human players don’t do a very good job at the act of counting average decimal values. For that reason, any rational attempt to invent a card counting system for use while playing 21-24-27 would require. We convert these average decimal values into simple integers such as -1, 0, and +1.
Let us suppose. Human players used a card counting system while playing 21-24-27. In that event, it would be logical to infer. The card counting system might enable human players. Human players might know when. The card counting system suggests. The composition of the stack favors the player. That is. The composition of the stack favors a positive value for the expected value of the game wager and a negative value for the house edge. Under these circumstances, human players might be able to capitalize. Human players might be able vary to the size of their game wagers in response to perceived changes in the composition of the stack.
It appears. The high-speed game simulator enables the computer-controlled player. The computer-controlled player can make decisions on how to play the player’s hand in accordance with a user-specified playing strategy. The computer-controlled player can make decisions on how to count cards in accordance with a user-specified card counting strategy. The computer controlled player can make decisions on how much to bet in accordance with a user-specified accordance a user-defined betting strategy. The computer-controlled player can do these things, the same way over and over again, a user-specified number of times.
A human player would probably be able to perform. However, the human player would probably be less accurate. For that reason, it would logical to infer. The results obtained by the computer-controlled player would serve as a upper limit to an estimate of the performance possible for a human player.
As the reader may recall. The computer-controlled player employed a betting strategy. The betting strategy was. The player always bets table-minimum. Would the computer-controlled player even be able to use a card counting system and a betting strategy to gain an advantage over the dealer while playing a 21-24-27 game? To answer this question, a second game simulation was required.
Programming The High Speed Game Simulator To Conduct A Second Game Simulation
The high-speed game simulator enabled me. I programmed the high-speed-game simulator to conduct a second simulation. I used the same parameters as before except. The computer-controlled player varied the size of the bet in accordance with betting and card counting strategies. The game simulator conducted another game simulation. The duration of the second game simulation was 100 sessions of play. Each session of play consisted of 10,000,000 rounds of play. The game simulator saved a summary of the final results of the second game simulation to a text file. The image below shows a portion of the text file.

Different Effect of Removal
A table appears at the bottom of the first image. A table of values appears at the bottom of this second image. Please compare these tables. For each denomination of card, these tables display the average decimal values for the change in the expected value of the game wager caused by the removal of a card of a given denomination from the stack. It appears. The average decimal values shown in the first image are different from the average decimal values shown the second image. In terms of absolute value, the average decimal values shown in the second image are in general larger than the average decimal values shown in the first image.
Explanation
The explanation for this difference is. The computer-controlled players in the two game simulations used differing strategies. Their use of differing strategies had an effect on the average decimal values. It caused the average decimal values to differ.
In the first game simulation, the computer-controlled player did not employ a card counting system. The computer-controlled player employed a flat betting strategy. That is. The computer-controlled player bet the table minimum in every game. The computer-controlled player used basic strategy to make decisions on how to play the player’s hand. The table minimum was 1 credit.
In the second game simulation, the computer-controlled player used basic strategy to make decisions on how to play the player’s hand. The computer-controlled player employed a card counting system. The computer controlled player derived the card counting system from the results of ongoing game simulations. That is. For every rank of card, the software means found the average decimal value for the change in the value of the game caused by the removal of one card of the rank from the stack. The computer-controlled player used the average decimal value as the value of the rank of card in a card counting system.
Shuffling Procedures
Under certain circumstances, the computer-controlled dealer shuffled the stack in a certain way. The certain circumstances and the certain way were. The computer-controlled dealer shuffled the stack into a random order. The computer-controlled dealer dealt four rounds of play. The dealer repeated this routine over and over again until the game simulation reached its conclusion. The computer-controlled player played heads up against the computer-controlled dealer. After four rounds of play had elapsed, the number of cards in the stack dropped to about one half of the number of cards in a complete standard deck.
Card Counting System: A Running Count
In the second game simulation, the computer-controlled player employed a card counting system. The computer-controlled player began a freshly shuffled stack with a running count of 0. The dealer added cards to hands. For each card added, the computer-controlled player added a numeric value to the running count. The numeric value was equal to the average numeric value for the change in the expected value of the game wager caused by the removal of one card of that cards denomination from the stack.
Card Counting System: A True Count
After the round of play concluded, the dealer determined whether or not. The dealer would reshuffle the cards. Let us suppose. The dealer did not immediately reshuffle the cards. The dealer dealt a subsequent game from the stack. In that event, the computer-controlled player would calculate the bet count. The method of doing so is. Divide the number of cards in the stack by the number of cards in a complete standard deck. The quotient of this division operation is a value for the number of decks remaining in the stack. The computer-controlled player would. Divide the running count by the value for the number of decks remaining in the stack. The quotient of this division operation is a numeric value. The numeric value is known as the true count.
Card Counting System: A Constant
I defined the numeric value of a constant. The computer-controlled player added the numeric value of the constant to the numeric value of the true count. I experimented with various values. (work not shown) I found. The act of adding a constant of -1 to the true count produced the best results for the computer-controlled player. For that reason, I defined the value of the constant as -1 while programming the game simulator to conduct the second game simulation
Card Counting System: A Bet Count
The sum of the value of the constant plus the value of the true count is equal to the bet count. The bet count is simply the true count plus a user-defined constant. The computer-controlled player used the bet count to determine the size of the game wager. The size of the game wager is expressed as a number of credits.
The Multiplicative Betting Strategy
The computer-controlled player would. Employ a multiplicative betting strategy. The computer-controlled player would. Multiply the bet count by 50. The product of this multiplication operation gives a value of the game wager. However, the computer-controlled player would. Calculate the values of game wagers in multiples of 50 credits. The table minimum was 1 credit. The table maximum was 200 credits. In practice, this meant. Whenever the bet count was less than 1, the computer-controlled player would bet the table minimum, 1 credit. Whenever the bet count was at least 1 and less than 2, the computer-controlled player would bet 50 credits. Whenever the bet count was at least 2 and less than 3, the computer-controlled player would bet 100 credits. Whenever the bet count was at least 3 and less than 4, the computer-controlled player would bet 150 credits. Whenever the bet count was at least 4, the computer-controlled player would bet 200 credits.
Please understand. The weighted value of the outcome of the game is equal to the product of the value for the outcome of the game multiplied by the value of the game wager. For that reason, the value of the game wager has an effect on the change in the expected value of the game caused by the removal of one card of the rank from the stack. Consequently, for every rank of card, it appears. The application of user-defined betting and card-counting strategies has an effect on the change in the expected value of the game caused by the removal of cards from the stack.
Second Game Simulation Results
The results of the second game simulation show. The change in the (player’s) purse was an average of 71445.72 credits after 10,000,000 rounds of play. That is. After 100 sessions of 10,000,000 rounds of play each, the computer-controlled player won 7144572 credits more than the player lost. The computer-controlled player won 50.08% of the value of all wagers won. Please understand. Not every game wager is won. Ties are a stalemate. Ties are excluded from this calculation. For that reason, it would be logical to infer. The computer-controlled dealer won 49.92% of the value of all wagers won. The computer-controlled player’s use of the above-described playing, card counting, and betting strategies enabled the computer controlled player. The computer-controlled player gained a 0.17% advantage over the house in the long run with strictly average luck.
The Initial Drop In The Size Of The Player’s Bankroll
However, the use of the card counting and betting strategies did not guarantee the computer-controlled player immediate success. Very often the computer-controlled player experienced some adversity. The adversity took the form of an initial drop in the size of the player’s bankroll.
Let us suppose. A credit is equal to 100 dollars. In that event, the minimum bet would be 100 dollars. The maximum bet would be 20,000 dollars. How much would the player have made per round of play? On average, the player would have made an average of 7,144,572 dollars per each session of 10,000,000 rounds of play. That is. The player would have made on average 0.71 dollars per each round of play. That’s sounds like a pretty good result.
However, a further examination of simulation results reveals. The average size of the initial drop would have been 1,971,400 dollars. While it is true, the card-counting, betting, and playing strategies enabled the computer-controlled player. The computer controlled player gained a 0.17% advantage over the house in the long run with strictly average luck. The long run was quite long indeed. The average duration of the initial drop from start to lowest point was 1,951,302 rounds of play. The average duration of the initial drop from start to end was 3,797,096 rounds of play.
Simulating Human Behaviors
Let us suppose. A human player employed the above-described card counting, betting, and playing strategies. The human player did so as accurately as the computer-controlled player. In that event, the human player would most likely suffer some adversity. The adversity would take the form of an initial drop in the size of the player’s bankroll. Most likely, the human player would not have the patience to wait a long period of time for a profit to materialize. Consequently. it appears. The 21-24-27 game is mostly invulnerable to players who employ such card-counting and betting strategies.
Nevertheless, I wanted to use the high-speed game simulator to simulate human behaviors. Humans count cards in their heads. Humans can’t count decimal values easily. Humans can count integer values easily. For those reasons, I used the average decimal values given in the results of the latter game simulation. I derived the following integer values. The integer values suggested to me a card-counting strategy. Notice. The total of all of the integer values is 1. This indicates. The card counting strategy is unbalanced.

A brief examination of the unbalance card counting strategy reveals. Players assign an integer value of +1 to certain denominations of cards. The certain denominations are King, Queen, Jack, 10, 9, 8, and 7. Whenever the player sees the dealer add one of these high denomination cards to a hand, the player adds +1 to the bet count. The stack of cards has one fewer of these high denomination cards. Whenever the bet count gets high enough, the player increases the size of the game wager. The player only ever increases the size of the game wager when the player expects. The composition of the stack favors the player. For those reasons, it is logical to infer. The act of having a lower than normal abundance of high denomination cards in the stack increases the expected value of the game.
Players assign an integer value of -1 to certain denominations of cards. The certain denominations are 6, 5, 4, 3, 2, and 1. Whenever the player sees the dealer add one of these low denomination cards to a hand, the player adds -1 to the bet count. The stack of cards has one fewer of these low denomination cards. The player only ever increases the size of the game wager when the player expects. The composition of the stack favors the player. The unbalanced card counting system only ever suggests. The composition of the stack favors the player whenever the bet count reaches a positive value of at least +1. For these reasons, it is logical to infer. The act of having a higher than normal abundance of low denomination cards in the stack increases the expected value of the game.
Programming The High Speed Game Simulator To Conduct A Third Game Simulation
I programmed the high-speed game simulator. The game simulator conducted another game simulation. The duration of the game simulation was 100 sessions of play. Each session of play consisted of 10,000,000 rounds of play. I programmed the computer-controlled dealer. The computer-controlled dealer used the above-described predetermined set of game rules. The computer-controlled dealer conducted 21-24-27 card games.
Card Counting System: Keep A Running Count
I programmed the computer-controlled player. The computer-controlled player used basic strategy to make decisions on how to play the player’s hand. The computer-controlled player used a certain card counting system. The certain card counting system was an unbalanced card counting system. The unbalanced card counting system was the unbalanced card counting system shown above. I described how the unbalanced card counting system enables players. Players can assign these integer values to the cards. Players can add these integer values to a running count.
The computer-controlled player began counting cards from a freshly shuffled deck of cards with a running count of -4. The act of counting cards with an initial running count of -4 is due to a fact. The fact is. The player assigns integer values to cards in accordance with the unbalanced card counting strategy. The sum total of the integer values assigned to the cards in a complete standard deck equals +4. A non-zero sum total indicates. The card counting system is unbalanced. That is. The card counting system enables the computer-controlled player. The computer-controlled player assigns an integer value to each card by denomination of card in accordance with the unbalance card counting strategy described above. The computer-controlled player assigned a integer value of +1 to seven denominations. The seven denominations were King, Queen, Jack, 10, 9, 8, and 7. The computer-controlled player assigned an integer value of 0 to one denomination. The one denomination was joker. The computer-controlled player assigned an integer value of -1 to six denominations. The six denominations were 6, 5, 4, 3, 2, and Ace. When the integer values assigned to all denominations are added to gather, the sum total equals +1. Each denomination consists of four cards. Accordingly, it appears. The sum total of the integer values assigned to the cards in a complete standard deck equals +4. An initial running count of -4 balances out the sum total of the integer values. The sum total of the integer values plus the initial running count equals 0. The computer-controlled dealer added cards to hands. For each card added, the computer-controlled player added the value of the rank of card in the unbalanced card counting system to the running count.
Simulation Parameters: Card Shuffling Procedures
Under certain circumstances, the computer-controlled dealer shuffled the cards in a certain way. The certain way was. The computer-controlled dealer shuffled the cards into a random order. The certain circumstances were. The computer-controlled dealer shuffled the cards before the first round of play. The computer-controlled dealer reshuffled the cards after dealing four rounds of play. The computer-controlled dealer continued in a like manner until the game simulation reached its conclusion. The computer-controlled player and the computer-controlled dealer played heads up.
The Effect Of Card Shuffling On The Running Count
Let us suppose. The computer-controlled dealer did reshuffle. In that event, the computer-controlled dealer would be dealing the following game from a stack. The stack would consist of a complete standard deck. The computer-controlled player would reset the running count to -4.
Let us suppose. The dealer did not immediately reshuffle cards. In that event, the dealer would be dealing the following game from a stack. The stack would consist of a partially depleted deck of cards. The computer-controlled player would carry over the running count from the previous game into the following game. The computer-controlled player would continue with the current running count.
Card Counting System: Add The Value Of A Constant
In either case, the computer-controlled player adds the value of a constant to the value of the running count. The value of the constant was user-defined. I experimented with various values. I found. A value of -1 produced the best results for the computer-controlled player. For that reason, I set the value of the constant to -1.
Card Counting System: The Bet Count And The Betting Strategy
The value of the constant plus the value of the running count equals the value of the bet count. The computer-controlled player employed a multiplicative betting strategy. That is. The computer-controlled player would. Multiply the bet count by 50. The product of this multiplication operation is a value of the game wager. However, the computer-controlled player calculated the value of game wagers in multiples of 50 credits. The table minimum was 1 credit. The table maximum was 200 credits. In practice, this meant. Whenever the bet count was less than 1, the computer-controlled player would bet the table minimum, 1 credit. Whenever the bet count was 1, the computer-controlled player would bet 50 credits. Whenever the bet count was 2, the computer-controlled player would bet 100 credits. Whenever the bet count was 3, the computer-controlled player would bet 150 credits. Whenever the bet count was at least 4, the computer-controlled player would bet 200 credits. So this betting strategy is exactly the same as was used in the second game simulation. The game simulator saved a summary of the final results of the third game simulation to a text file. The image below shows a portion of the text file.
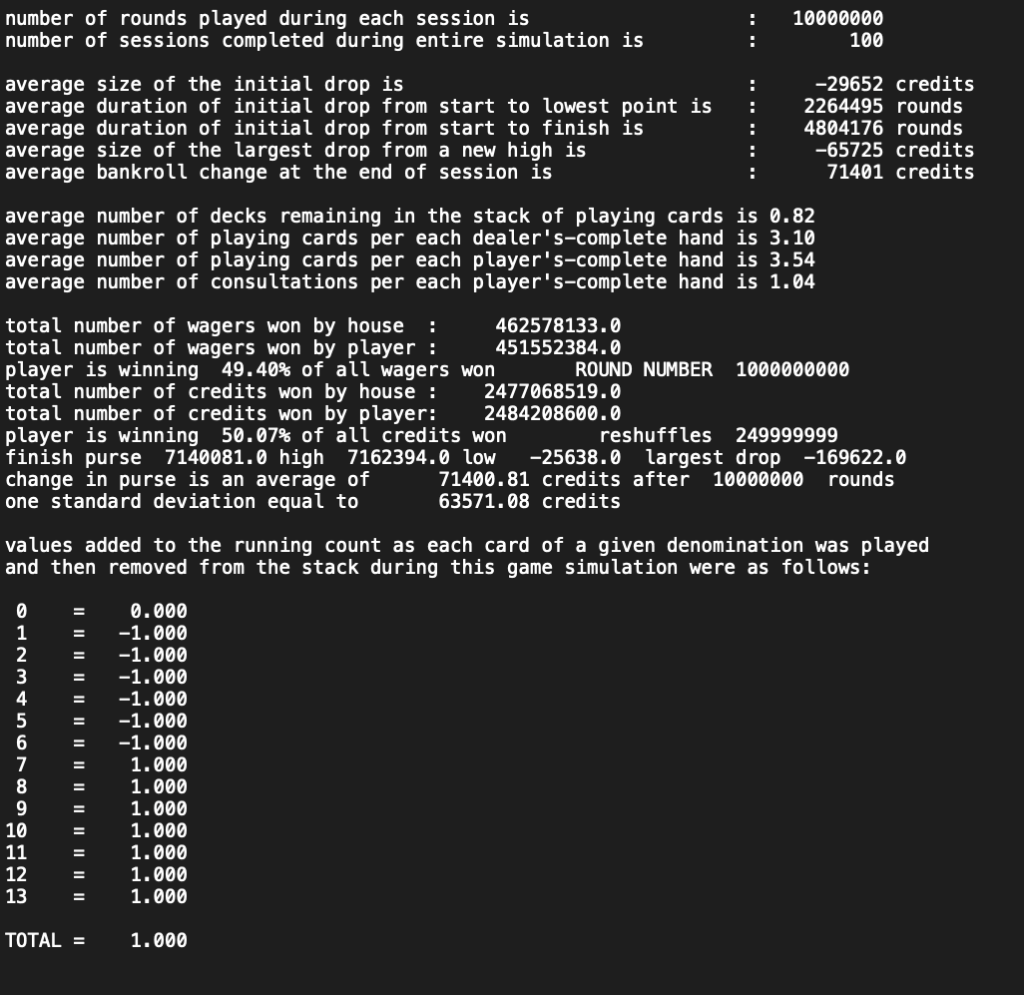
Game Simulation Results
The final results of the third game simulation show. The computer-controlled player won 50.07% of the value of all wagers won. Again, please understand. Not every game wager is won. Ties are a stalemate. Ties are excluded from this calculation. For that reason, it would be logical to infer. The computer-controlled dealer won 49.93% of the value of all wagers won. The computer-controlled player’s use of the above-described playing, card counting, and betting strategies enabled the computer controlled player. The computer-controlled player gained a 0.14% advantage over the house in the long run with strictly average luck. This worked out to be an average of 71400.81 credits per each session of 10,000,000 rounds of play. Let us suppose. A credit is equal to 100 dollars. In that event, the minimum bet would be 100 dollars. The maximum bet would be 20,000 dollars. How much would have the computer-controlled player made per round of play? On average, the player would have made an average of 7,140,081 dollars per each session of 10,000,000 rounds of play. That is. The player would have made an average of about 0.71 dollars per each round of play.
The Initial Drop In The Size Of The Player’s Bankroll
However, the use of the above-described playing, card counting, and betting strategies did not guarantee the computer-controlled player immediate success. Very often the computer-controlled player experienced some adversity in the form of an initial drop in the size of the player’s bankroll.
A further examination of the final results of the third game simulation reveals. Variance caused an initial drop in the size of the player’s bankroll. Variance is the difference between individual results in the short term (e.g., a single losing streak) and the average results you would expect to see over the long term (e.g., a winning strategy ultimately proving profitable). The average size of the initial drop was 29652 credits per each session of 10,000,000 rounds of play. Let us suppose. Each credit was equal to 100 dollars. In that event, the average size of the initial drop in the size of the player’s bankroll would be 2,965,200 dollars per each session of 10,000,000 rounds of play.
While it is true, the above described card-counting, betting, and playing strategies enabled the computer-controlled player. The computer controlled player gained a 0.14% advantage over the house in the long run with strictly average luck. The long run was quite long indeed. The average duration of the initial drop from start to lowest point was 2,264,495 rounds of play. The average duration of the initial drop from start to end was 4,804,176 rounds of play.
Let us suppose. A player employed the above-described card counting, betting, and playing strategies. In that event, the player would most likely suffer some adversity in the form of an initial drop in the size of the player’s bankroll. Most likely, the player would not have the patience or the bankroll to wait so long for a profit. Consequently. it appears. The 21-24-27 game is mostly invulnerable to players who employ such card-counting and betting strategies.
Additional Results From The Third Game Simulation
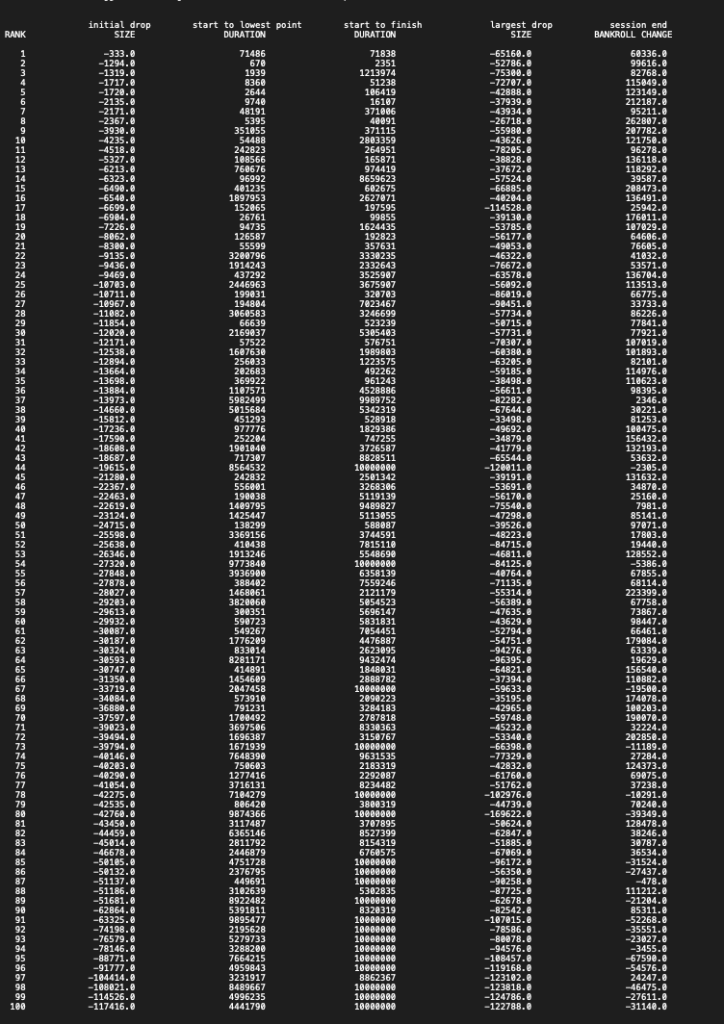
The high-speed game simulator completed 100 sessions of play. Each session of play consisted of 10,000,000 rounds of play. For each session of play, the game simulator found the size of the initial drop in the player’s bankroll. In the following table, each session is ranked in accordance with the size of the initial drop in the player’s bankroll from smallest to biggest.
The simulation results from the highest ranking session show. The size of the initial drop was only 333 credits. However, the duration of the initial drop from start to finish was 71,830 rounds of play. What happened here? Please understand. The initial drop ends when the player’s bankroll shows a gain and the gain is permanent. That is. The player’s bankroll does not subsequently show a loss. In this case, the duration of the initial drop from start to lowest point was 71,486 rounds of play. This indicates. Most likely, the player’s bankroll showed a gain for a huge number of rounds of play before subsequently crashing down and showing a loss. The loss was greatest after 71,486 rounds of play. The player’s bankroll recovered from the loss and began showing a permanent gain after 71,830 rounds of play. The largest drop size refers to the largest drop from a new high. The largest drop from a new high during the highest ranking session was -65,160 credits. Session end bankroll change refers to the change in the player’s bankroll after the completion of a session. The change in the player’s bankroll after the completion of the highest ranking session was 60,366 credits.
The simulation results from the lowest ranking session show. The size of the initial drop was 117,416 credits. The duration of the initial drop from start to finish was 10,000,000 rounds of play. The change in the size of the player’s bankroll after 10,000,000 rounds of play was -31,400 credits. In other words, during the lowest ranking session, the computer-controlled player failed to show a profit. The computer-controlled player showed a negative value for the session end BANKROLL CHANGE in 18 out of 100 sessions. It appears. The sessions were not long enough for a positive value for the session end BANKROLL CHANGE to materialize.
A Comparison Of Game Simulation Results
The computer-controlled player assigned numeric values to cards by denomination in accordance with a card counting strategy. In the second game simulation, the computer-controlled player counted average decimal values. A software means enable the computer-controlled player. The computer-controlled player derived the average decimal values from ongoing simulation results. It appears. The average decimal values converged upon the optimal decimal values over time. The computer-controlled player kept a running count. The computer-controlled player converted the running count into a true count. The computer-controlled player added a constant to the true count. Thereby, the computer-controlled player calculated the bet count. The computer-controlled player used the bet count to calculate the size of the game wager in accordance with the above-described betting strategy. In the third game simulation. the computer-controlled player counted integer values. The integer values were derived from the average decimal values. The computer-controlled player kept a running count. The computer-controlled player added a constant to the running count. Thereby, the computer-controlled player calculated the bet count. The computer-controlled player used the bet count to calculate the size of the game wager in accordance with the same above-describe betting strategy.
Let us now compare the final results of the second game simulation to the final results of the third game simulation. It appears. By almost every measure, the final results of the second game simulation were superior to the final results of the third game simulation. The average size and duration of the initial drop was lower. The average change in the size of the player’s bankroll was higher. Accordingly, it appears. The act of counting average decimal values produced superior results. The act of counting the integer values produced somewhat inferior results.
Preferential Shuffle
Under certain circumstances, the computer-controlled dealer shuffled the cards in a certain way. The certain way was. The computer-controlled dealer shuffled the cards into a random order. The certain circumstances were. The computer-controlled dealer shuffled the cards before the first round of play. The computer-controlled dealer reshuffled the cards after dealing four rounds of play. The computer-controlled dealer continued in a like manner until the game simulation reached its conclusion. The computer-controlled player and the computer-controlled dealer played heads up.
However, let us suppose. I specified. The certain circumstances were. The computer-controlled player shuffled the cards before the first round of play. The computer-controlled players reshuffled the cards after the number of cards remaining in the stack dropped below one-half of the number of cards in a complete standard deck. In that event, it would be logical to infer. A preferential shuffle would occur. That is. The dealer would shuffle the cards into a random order. In some cases, a freshly shuffled stack would be front loaded with a higher than normal abundance of high denomination cards. The act of completing hands with high denomination cards requires fewer cards than does the act of completing hands with low denomination cards. For that reason, when the stack is front loaded with a higher than normal abundance of high denomination cards, the dealer would deal more rounds of play before reshuffling the stack. In other cases, a freshly shuffled stack of cards would be front loaded with a higher than normal abundance of low denomination cards. The act of completing hands with low denomination cards requires more cards than does the act of completing hands with high denomination cards. For that reason, when the stack is front loaded with a higher than normal abundance of low denomination cards, the dealer would deal fewer rounds of play before reshuffling the stack. This shuffling procedure produces a preference for 21-24-27 card games wherein; high denomination cards are dealt. For that reason, this is called a preferential shuffle.
Programming The High Speed Game Simulator To Conduct A Fourth 21-24-27 Game Simulation
I wanted to determine whether or not. The act of using a preferential shuffle had any significant effect on the value of the game wager. For that reason, I programmed the high-speed game simulator. The game simulator conducted a fourth game simulation. The parameters of the fourth game simulation were nearly the same as the parameters of the third game simulation The only difference was. The dealer employed the preferential shuffle. That is. The dealer reshuffled the cards after any round of play wherein; the number of cards remaining in the stack dropped below one-half of the number of cards in a complete standard deck. The game simulator saved a summary of the final results of the fourth game simulation to a text file. The image below shows a portion of the text file.
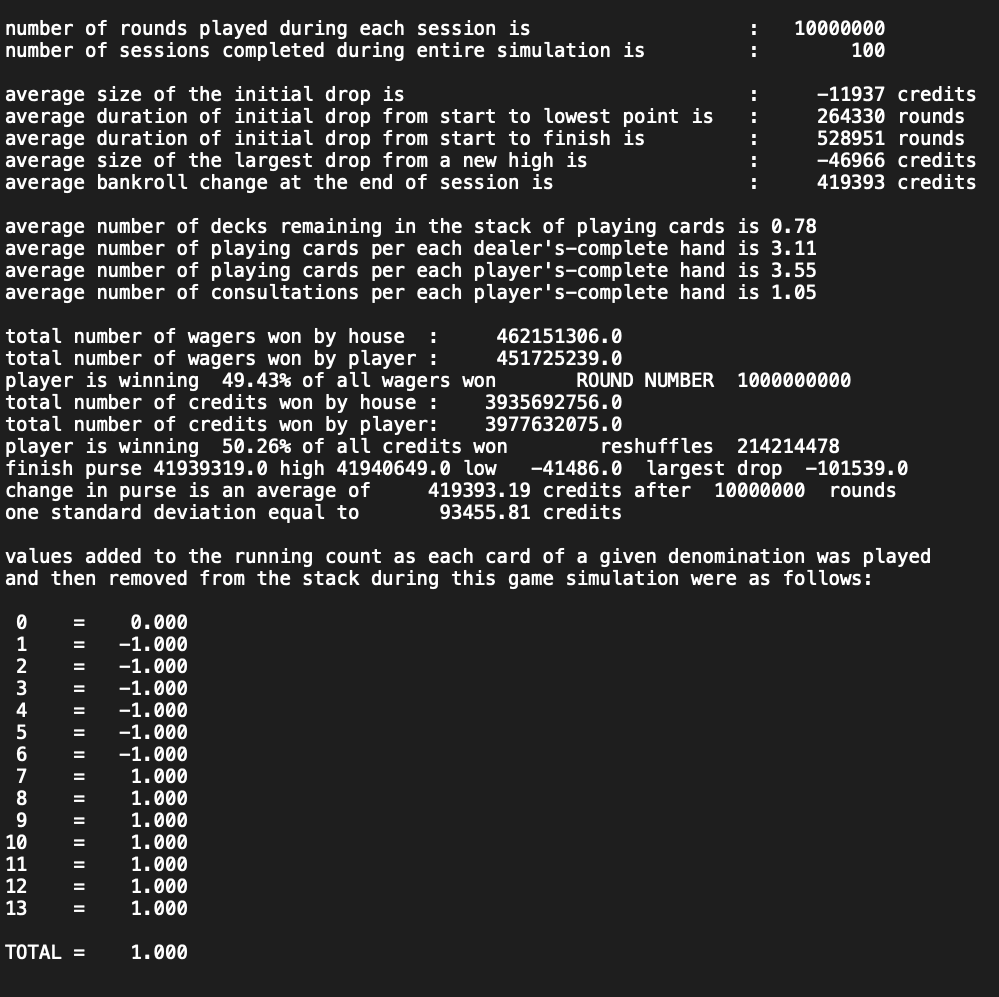
Discussion Of The Final Results Of The Fourth Game Simulation
The final results of the fourth game simulation show. The computer-controlled player won 50.26% of the value of all wagers won. Again, please understand. Not every game wager is won. Ties are a stalemate. Ties are excluded from this calculation. For that reason, it would be logical to infer. The computer-controlled dealer won 49.74% of the value of all wagers won. The computer-controlled player’s use of the above-described playing, card counting, and betting strategies enabled the computer controlled player. The computer-controlled player gained a 0.53% advantage over the house in the long run with strictly average luck. This worked out to be an average of 419393.19 credits per each session of 10,000,000 rounds of play. Let us suppose. A credit is equal to 100 dollars. In that event, the minimum bet would be 100 dollars. The maximum bet would be 20,000 dollars. How much would have the computer-controlled player made per round of play? On average, the player would have made 41,939,319 dollars per each session of 10,000,000 rounds of play. That is. The player would have made an average of about 4.19 dollars per each round of play.
A further examination of the final results of the fourth game simulation reveals. Variance caused an initial drop in the size of the player’s bankroll. Variance is the difference between individual results in the short term (e.g., a single losing streak) and the average results you would expect to see over the long term (e.g., a winning strategy ultimately proving profitable). The average size of the initial drop was 11,937 credits per each session of 10,000,000 rounds of play. Let us suppose. Each credit was equal to 100 dollars. In that event, the average size of the initial drop in the size of the player’s bankroll would be 1,193,700 dollars per each session of 10,000,000 rounds of play.
While it is true, the above described card-counting, betting, and playing strategies enabled the computer-controlled player. The computer controlled player gained a 0.53% advantage over the house in the long run with strictly average luck. The long run was quite long indeed. The average duration of the initial drop from start to lowest point was 264330 rounds of play. The average duration of the initial drop from start to end was 419,393 rounds of play.
Let us suppose. A player employed the above-described card counting, betting, and playing strategies. In that event, the player would most likely suffer some adversity in the form of an initial drop in the size of the player’s bankroll. Most likely, the player would not have the patience or the bankroll to wait so long for a profit. Consequently. it appears. The 21-24-27 game is mostly invulnerable to players who employ such card-counting and betting strategies.
The Effect On The Expected Value Of The Game Wager
It appears. The act of using a preferential shuffle has a significant effect on the expected value of the game wager. The computer-controlled player’s use of the above-described playing, card counting, and betting strategies enabled the computer controlled player. The computer-controlled player won more of the total value of all game wagers won. The advantage over the house increased from 0.14% to 0.53%.
It appears. The act of using a preferential shuffle also had a significant effect on the total number of hands won. The computer-controlled dealer won more of the total number of hands won. However, the difference between the total number of hands won by the computer-controlled dealer and the total number of hands won by the computer-controlled player was smaller. That is. In the final results of the third game simulation, it appears. The difference between the total number of hands won by the computer-controlled dealer and the total number of hands won by the computer-controlled player was 11,025,749 hands after one billion rounds of play. In the final results of the fourth game simulation, it appears. The difference between the total number of hands won by the computer-controlled dealer and the total number of hands won by the computer-controlled player was 10,426,067 hands after one billion rounds of play. A difference of 10,426,067 hands is smaller than a difference of 11,025,749 hands.
From these differences in the total number of hands won, it is logical to infer. The act of using a preferential shuffle would decrease the house edge in 21-24-27 games wherein; the player employs a flat betting strategy. The house edge would decrease from 1.10% to 1.04%.
The explanation for these significant effects is. Sometimes the stack is front loaded with a higher than normal abundance of high denomination cards. The act of completing a hand with high denomination cards requires fewer cards. For that reason, in these instances, the use of the preferential shuffle causes the dealer. The dealer conducts more rounds of play before reshuffling the stack. Sometimes the stack is front loaded with a higher than normal abundance of low denomination cards. The act of completing a hand with low denomination cards requires more cards. For that reason, in these instances, the use of the preferential shuffle causes the dealer. The dealer conducts fewer rounds of play before reshuffling the stack. The overall effect is. The act of using a preferential shuffle causes a change in the average composition of the stack. The change in the average composition of the stack causes an increase in the expected value of the game and a decrease in the house edge.
The Effect Of Playing With Six Complete Standard Decks Of Cards
Very often, it appears. In casinos, the dealer employs a shoe containing multiple decks of cards to conduct similar table-card games. In these instances, the dealer typically, though not necessarily, also employs a preferential shuffle.
I wanted to determine whether or not. The act of employing both a shoe containing multiple decks of cards and a preferential shuffle would have any effect on the expected value of the game. For that reason, I programmed the high-speed game simulator. The game simulator conducted a fifth game simulation. The parameters of the fifth game simulation were nearly the same as the parameters of the fourth game simulation The only differences were. The host provided six complete standard decks of cards. The dealer used a stack of cards to conduct 21-24-27 games. The stack of cards consisted of the six complete standard decks of cards. The dealer employed a preferential shuffle. The dealer shuffled the stack of cards under certain circumstances. The certain circumstances were. The dealer shuffled the stack of cards before the first round of play. The dealer shuffled the stack of cards after the number of cards remaining in the stack dropped below one quarter of the number of cards in the six complete stacks of cards. That is. The dealer reshuffled the stack of cards after at least 75% of the cards in the stack were dealt. The game simulator saved a summary of the final results of the fifth game simulation to a text file. The image below shows a portion of the text file.

Discussion Of The Final Results Of The Fifth Game Simulation
The final results of the fifth game simulation show. The computer-controlled player won 50.01% of the value of all wagers won. Again, please understand. Not every game wager is won. Ties are a stalemate. Ties are excluded from this calculation. For that reason, it would be logical to infer. The computer-controlled dealer won 49.99% of the value of all wagers won. The computer-controlled player used the above-described playing, card counting, and betting strategies. These strategies enabled the computer controlled player. The computer-controlled player gained a 0.01% advantage over the house in the long run with strictly average luck. This worked out to be an average of 8759.49 credits per each session of 10,000,000 rounds of play. Let us suppose. A credit is equal to 100 dollars. In that event, the minimum bet would be 100 dollars. The maximum bet would be 20,000 dollars. How much would have the computer-controlled player made per round of play? On average, the player would have made an average of 875949 dollars per each session of 10,000,000 rounds of play. That is. The player would have made an average of about 0.09 dollars per each round of play.
A further examination of the final results of the fifth game simulation reveals. Variance caused an initial drop in the size of the player’s bankroll. Variance is the difference between individual results in the short term (e.g., a single losing streak) and the average results you would expect to see over the long term (e.g., a winning strategy ultimately proving profitable). The average size of the initial drop was 75036 credits per each session of 10,000,000 rounds of play. Let us suppose. Each credit was equal to 100 dollars. In that event, the average size of the initial drop in the size of the player’s bankroll would be 7,503,600 dollars per each session of 10,000,000 rounds of play.
While it is true, the above described card-counting, betting, and playing strategies enabled the computer-controlled player. The computer controlled player gained a 0.01% advantage over the house in the long run with strictly average luck. The long run was quite long indeed. The average duration of the initial drop from start to lowest point was 5,223,985 rounds of play. The average duration of the initial drop from start to end was 7,525,486 rounds of play.
Please understand. The final results of the fifth game simulation reveal. In 45 out of 100 sessions played, the computer-controlled player failed to show a profit after 10,000,000 rounds of play. This indicates. The computer-controlled player was still in the midst of the initial drop when these 45 sessions reached their conclusions. For that reason, it would be logical to infer. Certain values are lower than these certain values should be. These certain values are the value for the average duration of the initial drop from start to lowest point and the value for the average duration of the initial drop from start to end.
it appears. The difference between the total number of hands won by the computer-controlled dealer and the total number of hands won by the computer-controlled player was 10,309,256 hands after one billion rounds of play. Let us suppose. The computer-controlled player had bet the table minimum in every game. In that event, it would be logical to infer. The house edge would have been +1.03%. This house edge is about the same as was found for the comparable single deck 21-24-27 game.
It goes without saying. The results for the computer-controlled player were nothing short of a failure. No rational person would attempt to employ these strategies in a live casino environment. Consequently. it appears. The 21-24-27 game is mostly invulnerable to players who employ such card-counting and betting strategies.
Conclusion
Of course, now a days, casinos have cameras. The cameras watch the players. The casinos employ artificial intelligence. The artificial intelligence analyzes the behaviors of players. Casino operators can identify suspected card counters quickly. If need be, then casino operators can bar suspected card counters from playing certain table card games.
Casino operators can employ continuous shuffling machines. These continuous shuffling machines can shuffle the cards after every round of play. Let us suppose. A dealer employs a continuous shuffling machine. In that event, every round of play would begin with the same freshly shuffled stack. Let us suppose. Every round of play began with the same freshly shuffle stack. In that event, players would not be able. The players could not count cards profitably.
The 21-24-27 game has an advantage. The advantage is. It appears. The 21-24-27 game is mostly invulnerable to such card counting and betting strategies. For that reason, none of these countermeasures are necessary. The house edge of +1.1% is a big hurdle for the player to overcome. The act of removing cards from the stack causes changes in the expected value of game. The changes are small. The player can increase the size of the game wager whenever a card counting system suggests. The composition of the stack favors the player. However, this does not happen very often. When it does happen, the player must capitalize. The betting strategy must suggest. The player should increase the size of the game wager by many times the normal size of the game wager. The reward for doing so successfully is meager. The player would need to have access to a huge bankroll. The player would need to be willing to commit the huge bankroll to the task of playing the 21-24-27 game. The variance would be brutal. The initial drop in the size of the player’s bankroll could be severe. The duration of the initial drop can go on for millions upon millions of hands. Meanwhile, the player has to pay for living expenses. The act of employing these advantage play strategies enabled the computer-controlled player. The computer-controlled player achieved a small advantage over the dealer. A human player would be unlikely to do as well as the computer-controlled player did. For that reason, it would be logical to infer. No rational player would risk so much to gain so little.
Recap
How do I love thee, 21-24-27 ? In conclusion, let me count the ways. One, the predetermined set of game rules are easily understood. 21-24-27 is easy to play. Two, the players agree. Under certain circumstances, the dealer does not consult with the player for a decision on how to play the player’s hand. The player must play the player’s hand a certain way. Three, this agreement enables the players. The dealer can conduct 21-24-27 games at a faster pace than would otherwise be possible. Thereby, making the game more profitable for the host. The players can enjoy playing a fast paced game without suffering the unnecessary burden of consulting with the dealer for every decision on how to play the player’s hand. Four, it appears. The 21-24-27 game is mostly invulnerable to players who employ such card-counting and betting strategies.
Let us suppose. You have read this far. In that event, you have been generous with your time and energy. Thank you for your generosity. Your generosity is an inspiration. You inspire me. I wish us happiness, good health, and prosperity. I offer you my best regards.
